今年度の慶進中学2年コースは、学年末試験をひかえ、最終段階となりました。
日々、学年末試験に向けた学習を行っておりますが、慶進中学数学の幾何2では立体の切断問題が扱われます。
人間の感覚では平面で立体をとらえることはとても難しいため、平面図で理解できるようにするための重要なポイントを1つひとつ解説し、積み上げてきました。
立体の切断を理解するうえで基本的なものとして、
①同一平面上の点を結ぶ(異なる平面上の点は結んではいけない)
②ある面にできた切断線と、他の平行な面にできる切断線は平行になる
というポイントを実感する必要があります。
この2点を、立体の模型を用いながら説明したり、易しい問題からトレーニングしたりし、その後、徐々に難しい問題に応用していくと、力のある生徒はどんどん理解が進み、苦手だった立体問題が解けるようになっていきます。
また、錐台の体積の計算に関する重要ポイントを学習することでも、多くの難しめの立体の問題が解けるようになることを確認しました。
たとえば、傍用問題集のCレベルの問題の中に、正八面体の切断問題があります。
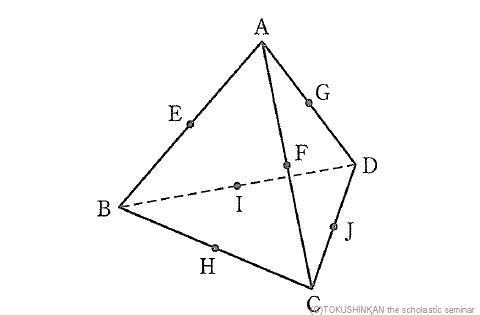
正四面体ABCDにおいて、その他の点はすべて各辺の中点で、点EFGHIJを頂点とする正八面体を点AHJを通る平面で切断したとき、点Fを含む立体の体積を求めよ、というものです。
問題集の解説では、三角錐の高さを求めることで直接体積を求める試みが紹介されていますが、これが難解(なかなかこういうアプローチに気づかない方法)で、解説が23行もあるのですが、それらを見てもその解説を求められることが毎年のようにあります。
しかし、これは私の授業の中で教えてきた上記のポイントと、錐台と相似の考え方を使うと、解き方の手順は2~3行程度で表現できますし、数式も解説より少ない行数で解くことができます。
結果はもちろんどちらも同じ値となるのですが、数学でのアプローチの仕方によってはこうも解き方が変わるものだということが実感できる、いい問題だと思います。
生徒たちが「なるほど」と納得する姿を見て、数学の面白さが伝わった気がしました。